| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- ...args
- .toLocalString()
- 1주차
- 2020년 준비
- 2주차
- 4주차
- 5주차
- array
- array method
- async
- authentication
- AWS
- codestates
- commit
- Cookie
- CSS
- Data Structre
- Data Structure
- DataSturcutre
- Date.now()
- DB에 사진 저장하기
- Dev log
- DOM
- EC2
- EC2로 웹 만드는 방법
- EC2와 S3 연결하기
- element
- Es5
- ES6
- event 객체
- Today
- Total
souvenir
[JS]바빌로니아 법을 이용해서 제곱근 구하기(Math.Sqrt 없이) 본문
0. 들어가며
JS에서 제곱근을 구하는 것은 간단한 일이다. Mat.sqrt()을 활용하면 나오기 때문이다.
그러나 새로운 방식으로, 수학의 원리를 이용해 풀고싶은 생각이 들때도 있다. 4나 9의 제곱근을 구하는 것은 쉬운 일이지만 2의 제곱근만 해도 무한수이기에 쉽게 구하기 쉽지 않다. √2가 1과 2 사이의 숫자라는 것을 이용해 대략의 근삿값을 추측할 수 있을 뿐이었다. 과거 학창시절을 돌아보면 이런 두 수 사이의 범위를 활용하여 3√2와 2√3 중 어떤 숫자가 더 큰가를 비교하는 시절도 있던 것 같다.
옛날 사람들은 위와 같은 방법으로 근삿값을 구하는 공식을 만들었는데 이를 '바빌로니아 법'이라고 한다.
1. 바빌로니아 법이란
※ 출처 : https://ko.wikipedia.org/wiki/%EB%B0%94%EB%B9%8C%EB%A1%9C%EB%8B%88%EC%95%84_%EB%B2%95

위 링크에 대한 예시가 이해가 되지 않아서 몇번 풀어보았다.
예시가 필요하신 분들은 아래 접은글 클릭
양의 실수 2에 대한 제곱근을 구해보고자 한다.
여기서 양의 실수를 a로 설정하였고, 초기값 x제로를 1로 설정해 보았을 때 아래와 같이 나온다.
x의 값을 무한으로 실행해 볼 수록(lim x->∞) 근삿값은 더욱 가까워짐을 알 수 있다.
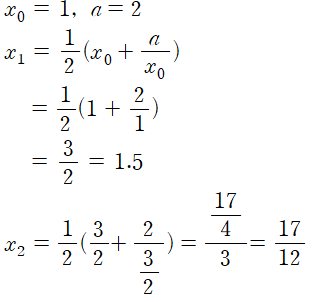
쉽게 이야기하면 이런 방식이다.
1) 양의 실수 6(변수 a)에 대해 √6의 근삿값을 구한다면
2) √6은 2와 3 사이의 숫자임을 예상할 수 있다. 임의로 2.5라고 가정했을 때,
2-1) 그 결과는 6.25이다.
3) 이를 활용해도 무리가 없다면 괜찮겠지만 오차범위가 크기에 임의의 수를 조금씩 줄여서 확인해 볼 수 있을 것이다.
3-1) 그 줄이는 범위를 바빌로이나 법은 위와 같은 공식으로 만든것이고, 알고리즘에서 활용한다면 오차범위를 설정해 그에 맞게 줄이는 방법이 있을 것이다.
1-1) 뉴턴-랩슨 방법 활용
양의 실수 a에 대한 제곱근 아래와 같이 표현할 수 있을 것이고,
이는 첫번째 식에서 N에 대한 해가 a의 제곱근과 같다는 것을 알 수 있다.
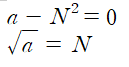
이런 점을 활용하여 이차방정식의 해의 근삿값, 혹은 (거의 같은 말이지만) 특정 함수의 역함수를 구하고자 활용되는 뉴턴-랩슨 방법을 활용하는 사람들도 있다. 문제는 이를 활용하기 위해서는 '점화식'이라는 개념이 필요한데 이것까지 이해하기는 어려워서 일단 C언어로나마 푸신 분의 알고리즘을 활용해보았지만 이분도 코드 오류가 많아서 제대로 돌아가지 않았다. ( 출처 : https://tyeolrik.github.io/data_structure/2017/01/21/7-newton-raphson-method-algorithm.html)
그 외에 다양한 글들을 검색해보았지만 대부분 C언어를 활용한 알고리즘 문제였기에 참고하기는 어려웠다.
그래서 다시 처음으로 돌아가 바빌로니아 법 자체를 다시 점검해보게 되었다.
2. 다시 바빌로니아 법을 활용하여 알고리즘 설정하기
이를 활용하면서 전제를 정리해 보았다.
1) 임의의 양의 실수인 a는 두 제곱수 사이에 존재한다.
2) 무한으로 돌리는 것은 무한 루프에 빠질 수 있으므로 일단 소수 둘째자리까지 중 근삿값을 구한다.
이를 수도코드로 정리해보자면 아래와 같다. (파라미터 : num)
1) 임의의 초기값(est)이 있다.
2) 이 초기값(est)의 제곱이 num과 같다면 return
3) 다르다면 초기값(est)에 0.01씩 더해주기 (소수 둘째 자리 중에서 가장 근삿값을 구하기 위해서)
3-1) 3번을 est와 num이 같거나 거의 비슷해질(소수 둘째자리 범위 내에서) 때까지 돌리기
3-2) toFixed, Number를 활용하여 소수 둘째자리까지의 숫자를 반환하기
이를 코드로 적어보면 아래와 같다.
//초기 추측값의 함수
//num은 어떤수의 제곱수 사이에 존재한다.
function squareroot(num) {
var lo = 0, hi = num;
while(lo <= hi) {
var mid = Math.floor((lo + hi) / 2);
//제곱수 사이의 중간값을 num의 제곱근이라고 임의로 가정(hi)
if(mid * mid > num) hi = mid - 1; else lo = mid + 1; } return hi; }
//hi의 제곱이 num인지 확인
function computeSquareRoot(num) {
let est = squareroot(num);
if(Math.pow(est) === num){
return est;
} else{
while(est*est < num){
//아니라면 다시 재귀함수 돌기
//이 재귀는 guess와 num의 오차가 플마 0.01보다 작을 때 끝내기
est += 0.01
}
}
return Number(est.toFixed(2));
}
3. 피드백
1) 초기값에 대해
초기값은 임의로 설정해도 된다고 하는 문서가 많았는데 더 정확하게 하고 싶은 욕심(?) 때문인지, num이 특정 수 사이라는 것을 알 수 없기에 가변적으로 설정해줘야 한다는 강박 때문인지 초기값을 설정하는 함수에 너무 많은 시간을 투자하였다. 결론은 사실 초기값은 그냥 '1'로 설정해도 돌아간다는 점. 오히려 초기값 설정 때문에 코드가 정리되지 못한 것 같다는 생각이 든다.
(이럴 때마다 느끼는 것이지만 JS가 생각보다 많이 느슨하게 적어도 인식하는 것 같다는... 물론 이 문제와는 관련 없는 특성이겠지만)
2) 알고리즘 설정에 대해
처음 이 문제를 마주했을 때는 사실 '실전에서 이런 것을 부딪힐 일이 없을텐데...'라는 생각에 귀찮다는 생각도 들었고, 여러 수학 공식을 부딪히면서 포기하고 싶다는 생각도 들었지만 생각보다 간단한 접근, 혹은 초기의 생각으로 내가 직접 코드를 만들어보는 것에 많은 성취감을 느꼈다.
3) 도전하는 정신
하지만 매일 할만한 것은 아니야
